This user has no status.
This user has no status.
Well-Known Member
We can. It would be that great a change to the RC calculations. In addition there is much more computing power available today than there was 10 years ago so computer power and memory are not a problem anymore.
On a recent thread I initially thought it would be a great idea to score 3-0 wins higher than 3-1 wins. I did the math, it took me only a few minutes to get the shocking result and more time to pretty print it.
In short scoring 3-0 wins differently than 3-2 wins is something that I don't think most TT players would want or are ready for.
Below are calculations of the probability of winning games for best 3 out of 5. No big deal yet. The shocker occurs when one player is much better than the other. I start with the assumption that the best player will win 11 out of 12 matches. That is approximate difference of 138 ratings points which isn't much. From the probability of winning the match I can calculate probability of winning each game. Then I calculate the probability for
each win loss combination. Notice all the probabilities must add up to 1 and the probability of winning 3-0, 3-1 and 3-2 must add up to the probability of winning the match. This is my sanity check.
There are two ways of looking at this.
1. One is to multiply the probability of winning a game * games played . This is relatively simple.
For example compare a 3-5 win to the expected wins 5*p.game=3.85. . In this case the winner did not does well as expected. Should the winner actually have his ratings points go up or stay the same when he didn't perform up to the expected level for the ratings difference?
Another example. Compare a 3-0 win to the expected wins. 3*p.game=2.31 . In this case the higher player did slightly better than expected. Maybe he deserves more points than what the current RC system would provide.
2. The second method involves adding up the probabilities.
A 3-2 win involves adding up the probabilities for 0-3, 1-3, 2-3 and finally the 3-2 win. The sum is less that 0.5 which means the winner didn't do as well as expected and should maybe lose points.
Now when the ratings are much much closer to being equal the distribution of win combinations is closer to symmetrical binomial function and would work out much closer to the way people would expect.
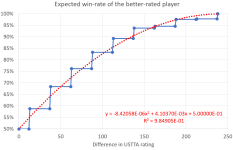
Look at the chart below. The calculations are not too difficult.
The question I have is does anybody really care? People usually oppose change. That is clear to see. People usually don't like 'better' if they can't see why it is better for them.
I just thought I would but this 3-0 and 3-2 issue to sleep forever.

On a recent thread I initially thought it would be a great idea to score 3-0 wins higher than 3-1 wins. I did the math, it took me only a few minutes to get the shocking result and more time to pretty print it.
In short scoring 3-0 wins differently than 3-2 wins is something that I don't think most TT players would want or are ready for.
Below are calculations of the probability of winning games for best 3 out of 5. No big deal yet. The shocker occurs when one player is much better than the other. I start with the assumption that the best player will win 11 out of 12 matches. That is approximate difference of 138 ratings points which isn't much. From the probability of winning the match I can calculate probability of winning each game. Then I calculate the probability for
each win loss combination. Notice all the probabilities must add up to 1 and the probability of winning 3-0, 3-1 and 3-2 must add up to the probability of winning the match. This is my sanity check.
There are two ways of looking at this.
1. One is to multiply the probability of winning a game * games played . This is relatively simple.
For example compare a 3-5 win to the expected wins 5*p.game=3.85. . In this case the winner did not does well as expected. Should the winner actually have his ratings points go up or stay the same when he didn't perform up to the expected level for the ratings difference?
Another example. Compare a 3-0 win to the expected wins. 3*p.game=2.31 . In this case the higher player did slightly better than expected. Maybe he deserves more points than what the current RC system would provide.
2. The second method involves adding up the probabilities.
A 3-2 win involves adding up the probabilities for 0-3, 1-3, 2-3 and finally the 3-2 win. The sum is less that 0.5 which means the winner didn't do as well as expected and should maybe lose points.
Now when the ratings are much much closer to being equal the distribution of win combinations is closer to symmetrical binomial function and would work out much closer to the way people would expect.
Look at the chart below. The calculations are not too difficult.
The question I have is does anybody really care? People usually oppose change. That is clear to see. People usually don't like 'better' if they can't see why it is better for them.
I just thought I would but this 3-0 and 3-2 issue to sleep forever.

Last edited: